Απάντηση

Η απάντηση είναι (b); Η μπίλια στο διάδρομο με τη «βύθιση» κερδίζει τον αγώνα δρόμου. Οι δύο μπίλιες πηγαίνουν μαζί στο πρώτο τμήμα της διαδρομής. Καθώς η άλλη μπίλια βυθίζεται η οριζόντια ταχύτητά της αυξάνεται και έτσι αρχίζει να παίρνει κεφάλι! Όταν επιστρέψει στο αρχικό οριζόντιο επίπεδο έχει επιβραδύνει και επιστρέψει στην αρχική οριζόντια ταχύτητα… αλλά παρ’ όλα αυτά ποτέ δεν πηγαίνει πιο αργά από την μπίλια που κινείται στον επίπεδο διάδρομο. Οι δύο μπίλιες κινούνται στο τελικό τμήμα του διαδρόμου με την ίδια ταχύτητα, αλλά η μπίλια του «βυθισμένου» διαδρόμου, έχει ήδη πάρει κεφάλι και κερδίζει τον αγώνα!

Κάνοντας Click με το ποντίκι στη φωτογραφία κάτω μπορείτε να δείτε σε φιλμ τον αγώνα δρόμου!

Το ίδιο ακριβώς πράγμα συμβαίνει όταν δύο άνθρωποι βαδίζουν μεν τον ίδιο ρυθμό, ο ένας δίπλα στον άλλο σε έναν επίπεδο δρόμο. Ξαφνικά ο ένας απ’ τους δύο αποφασίζει να επιταχύνει για μικρό χρονικό διάστημα και μετά επιστρέφει στον αρχικό ρυθμό βηματισμού. Αυτός που επιτάχυνε θα προηγηθεί και επιστρέφοντας στον αρχικό ρυθμό βηματισμού θα έχει κερδίσει ξεκάθαρα μια διαφορά σε σχέση με τον άλλο που δεν επιτάχυνε.

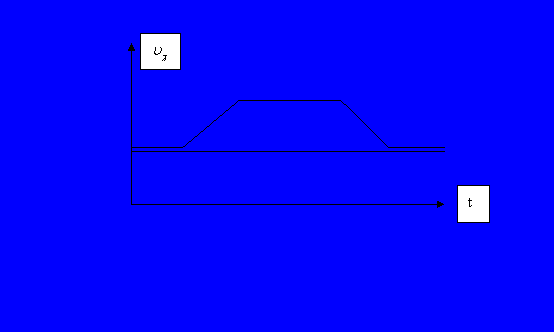
Ένας πιο μαθηματικός τρόπος να δούμε το πρόβλημα αυτό, είναι να σχεδιάσουμε τη συναρτήσει του χρόνου για τις δύο μπίλιες. Το εμβαδόν κάτω από το διάγραμμα δείχνει την οριζόντια μετατόπιση κάθε μπίλιας.

---